Big O Notation Put Simply

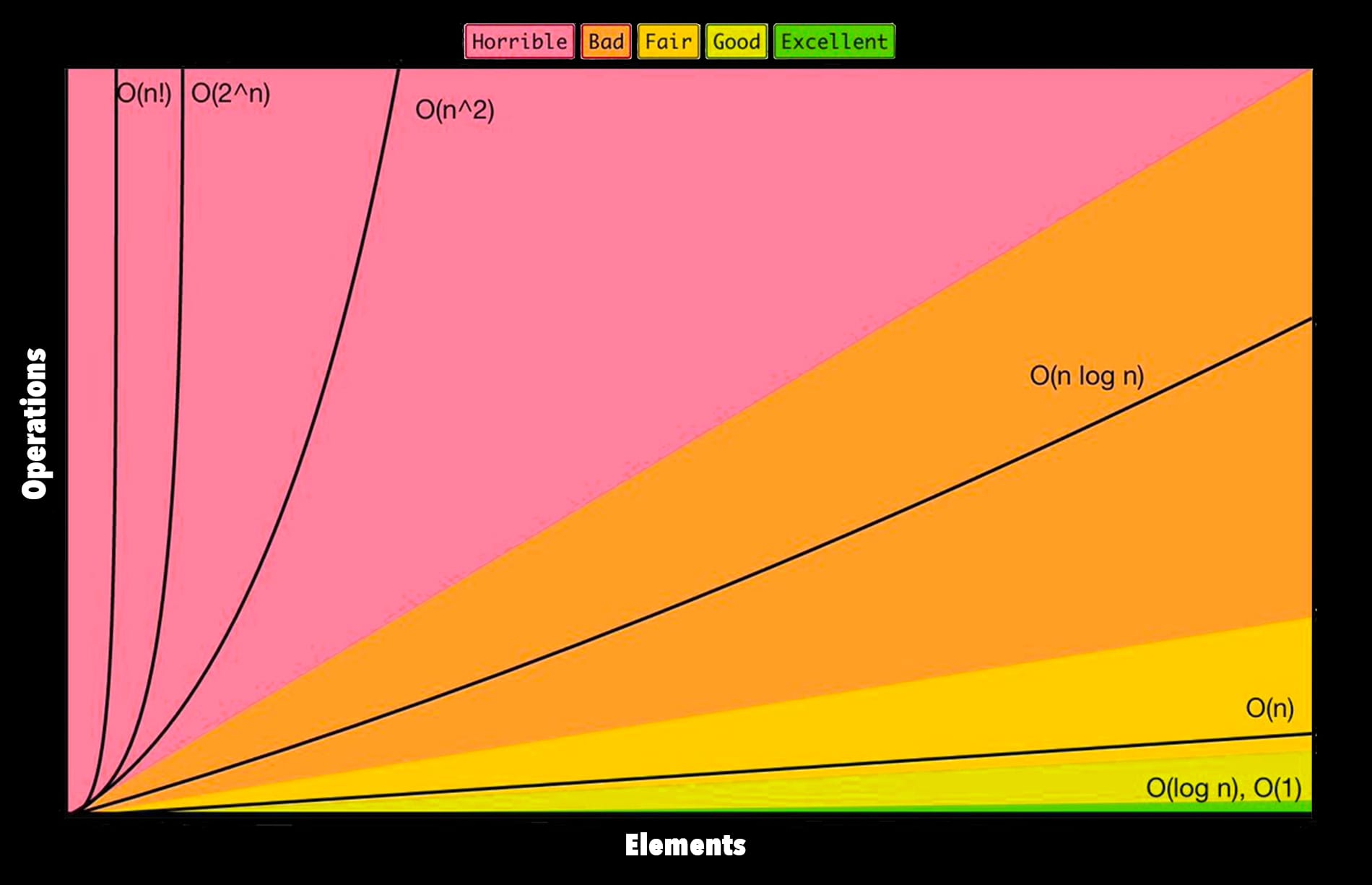
“Big O” notation is called this because it’s written something like O(n), and serves as a measure of efficiency of a particular algorithm. It’s a way of explaining how much a particular piece of code will suffer when put under load.

The the meaning of the “O” appears to be purely historical. So don’t get caught up on that.

I’ll do a few examples in ruby to show how this works.

O(n) or O of n

Here we have a method with the complexity O(n), which means that it will take longer based on how much information you put in it, on a linear scale.

# Create a large something we can iterate over
many = 1..1_000

def o_of_n(arg)
  arg.each { |i| puts i}
end

o_of_n(many)

O(n^2) or “O of n squared”

This one will square the amount of time it takes based on the same data. Assume the same setup as above. In other words, it takes 1000 times longer to run than the last example.

def o_of_n_squared(arg)
  arg.each do |i|
    arg.each do |n|
      puts(i,n)
    end
  end
end

o_of_n_squared(many)

O(a+b)

Becuase this method does two things in sequence, we add the two together.

a = 1..1_000
b = 1..10_000

def o_of_a_plus_b(a, b)
  a.each { |i| puts i}
  b.each { |i| puts i}
end

O(1) Does not change complexity based on the input

You’ll notice our method in this case doesn’t actually use the input at all. Increasing the amount of data input into the method changes nothing.

many = 1..1_000_000

def o_of_one(arg)
  2 + 2
end

o_of_one(many)